100+ Data Structures Related Questions

Generally students are asked to write programs which solve simple problems and the small amount of data. Therefore, they need not concern themselves about how the data are stored in computer’s main memory and how slowly or quickly the operations of retrieval and updations are performed.

However, when a complex and time-consuming problem is to be solved or when a large amount of data is to be used then it is very important that the data be organized in main memory so as to give faster access to data and the program be written accordingly.

Also Read:

• Cyber Security and Cyber Forensics – Interview Questions
• List of Most Important 500+ DBMS Interview Questions
• Top 250+ Technical Software Engineering Interview Questions
• Top Questions to Ask During a Computer Forensics Interview
• Top 77 Linux Interview Questions to Ask Candidates
• A to Z – Computer Security Terms and Definitions
• Top 50 Software Engineering Books To Read in 2021
• Important Terms Related To Software Engineering
• [Top 30] Checkpoint Firewall Questions with Answers
• Information Security Policy Related Questions with Answers
• Wireless Networks – Questions With Answers
• 100+ Computer and Network Security Abbreviations
• Windows Server 2016 – Multiple Choice Questions (MCQ) With Answers

Otherwise, main memory space as well as computer time required for various operations may be wasted. In main memory, time to access any location is the same whereas time to access any location is not the same on secondary storage, therefore organization of data in main memory and organization of data in secondary memory ave been discussed separately.

Here is the list of few Data Structure related questions:

1. Define
   • Data Item
   • Record
   • File
   • Data Structure
2. Explain various data structure operation.
3. What is the need for data structure ?
4. Differentiate between
   • Linear and Non-Linear data structure
   • Homogenous and Non- Homogenous data structure
   • Primitive and Non-Primitive data structure
   • Static and dynamic data structure
5. What are the various memory management techniques ? Explain
6. Define an algorithm. Write the characteristic of an algorithm.
7. Briefly describe the notions of
   • The complexity of an algorithm.
   • The space time tradeoff of algorithms
8. Define string and explain the string operation by giving suitable examples.
9. Write the algorithm for linear search and find its complexity.
10. Briefly describe the big O notation.
11. Explain various methods to store a string in memory.
12. What do you mean by algorithm complexity? How it is measured?
13. What is the role of time-space trade off.
14. Define
    • Array
    • Stack
    • Queue
    • Linked List
15. What is a Pointer? Explain the use of pointer by using example.
16. What is a Record? How can you represent a file in memory?
17. Define an array. Explain the sequential allocation method.
18. Derive the formula to find the address of elements of one-dimensional array.
19. Given the following linear arrays :
    • A [-5 : 18], B [1967: 2002]
      Find the number of elements in each of the arrays A and B.
20. Given the base address of array A [200 : 250] as 200 and size of each element is 3 words of memory, find addresses of A [215] and A[241].
21. Discuss the various operation on linear array.
22. Write an algorithm for inserting an element into a linear array.
23. Write an algorithm for deleting an element from a linear array.
24. Explain sequential representation of two-dimensional arrays and derive the formula for address computation of elements of two-dimensional array. A is a two-dimensional array with 25 rows and 4 columns. Each element of array is stored in 4 memory locations. If base address is 500, then compute the location of A [12, 3]. The organization is row-major.
25. Assume that a two-dimensional array A has been stored column-wise. If the element A [2, 2] is stored at location 130 and A [7, 5] at location 156, find out the location where the elements A [6, 6] be located. Each element requires one byte of storage. Can you find the number of rows and columns of the
    array A.
26. Suppose A [2 : 8, – 4 : 1, 6 : 10] is a multi-dimensional array. Suppose base address is 200 and there are 4 words per element. Find the position of the element A [5, -1, 8] when element of the array are stored rowwise.
27. Explain general multi-dimensional array.
28. Explain the sparse array. How can you store the sparse array in memory? Explain by giving suitable example.
29. State the limitation of Arrays.
30. What is a stack? Describe any two applications of stack.
31. What are the disadvantages of using array representation of stack?
32. Define and explain linked stack.
33. Write algorithm of PUSH and POP Operations.
34. Write algorithm to perform following operations on linked stack
    • PUSH
    • POP
35. Explain the method of evaluating postfix expression by giving suitable example.
36. Explain the procedure for transforming infix expression into postfix expression by giving suitable example.
37. Describe the concept of Polish notation.
38. Translate by inspection and hand each infix expression into its equivalent prefix expression.
    • (A-B) (D*E)
    • (A- B ↑ C) / (D – E) + F
39. Translate the infix expression
    • ( (A+B) * C) ↑ (D – E)
      into its equivalent postfix expression.
40. Evaluate the following postfix expression.
    • E = 5 6 2 + * 8 4 / –
41. Describe the algorithm of Tower of Hanoi.
42. What is Recursion ? Write the recursion algorithm and iterative algorithm for finding the factorial of a number N.
43. Write an algorithm for matching of parenthesis
44. Check the following expressions of nested parenthesis using stack.
    • x = ( () () )
    • x = ( ( ( ) )
45. Explain the various drawbacks of array.
46. What is linked list ? How can you represent a linked list in memory ?
47. Explain various operations of linked list.
48. Write the algorithm of traversing a linked list.
49. Write the algorithm of searching an element from a linked list.
50. Write the algorithm of searching an element from a sorted linked list.
51. Explain the insertion and deletion operations of linked list by giving suitable example.
52. Describe the concept of Free-Storage list.
53. Explain the concept of Garbage collection.
54. Write the algorithm of a linked list for
    • insertion at the beginning
    • insertion at the end
    • insertion after a given node
    • insertion into sorted linked list
55. Write the algorithm for copying operation of a linked list.
56. Write the deletion algorithm of a linked list.
57. Explain the advantages and disadvantages of circular list.
58. What is a doubly linked list ? How can you represent a doubly linked list in memory.
59. Explain the insertion and deletion operations of a doubly linked list by giving suitable examples.
60. Write the insertion algorithm of a doubly linked list.
61. Write the deletion algorithm of a doubly linked list.
62. Write the insertion and deletion algorithm of a two – way header list.
63. Explain the various application of linked list.
64. Describe the difference between sequential and linked storage allocations.
65. Distinguish between linear and non-linear data structures.
66. Define Queue. Give some examples of queues in computer.
67. Explain the difference between stack and queue.
68. Write the algorithm of INSERT and DELETE operation of the queue.
69. Explain the difference between queue and circular queue by giving suitable example.
70. Write the algorithm of insert and delete operation of circular queue.
71. What do you mean by deque and priority queue?
72. State some applications of queue.
73. What do you mean by linked queue?
74. What are the advantages of linked representation of queues over array representation of queues?
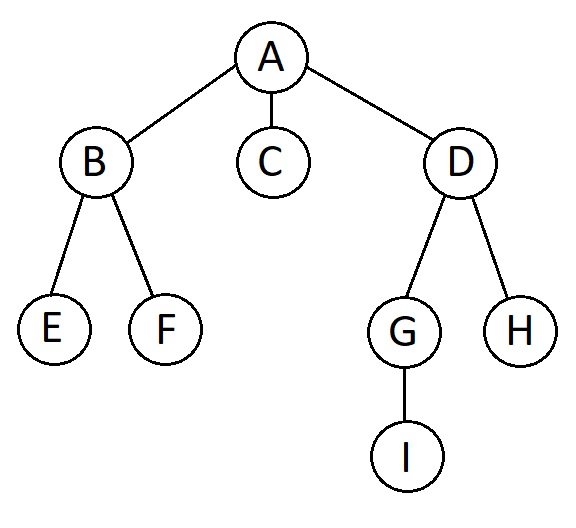
75. Define tree and write the properties of a tree.
76. Give
    • level,
    • degree and
    • height of each node of the following tree :
      
77. Define binary tree, full binary tree and strictly binary tree. Write the properties of binary tree also.
78. Explain the various methods of representation a binary tree in memory.
79. Explain the various methods of tree traversal by giving suitable example.
80. Write the algorithm of preorder, Inorder and postorder traversal.
81. Describe binary search trees and its applications.
82. Write the algorithm for searching and inserting a node in binary search tree.
83. Write the algorithm for deletion from a binary search tree.
84. Draw a diagram of a binary tree T if the preorder and inorder traversal of T yield the following sequence of nodes.
    Inorder : E A C K F H D B G
    Preorder: F A E K C D H G B
85. Consider the algebraic expression
    E = ( 2 m+n) (3 a – b)²
86. Draw the tree which corresponds to the expression E.
87. Suppose the following list of letters is inserted in order into an empty binary search tree
    J R D G T E M H P A F Q
    Find the final tree T.
88. Given the following binary search tree. Find the tree after the node G is deleted.
    
89. Explain the Traversal Algorithms using stack.
90. What do you mean by Searching? What are its types?
91. Explain Linear and Binary Search using examples.
92. Write an algorithm of Linear Search.
93. Write an algorithm of Binary Search.
94. Distinguish between Linear and Binary Search.
95. What do you mean by Sorting? What are its types?
96. Explain Selection and Bubble Sort by using examples.
97. Write an algorithm of Selection Sort.
98. Write an algorithm of Bubble Sort.
99. Explain Insertion Sort. Write its algorithm also.
100. Explain algorithm of Merge Sort.
101. Explain Quick Sort.
102. Write an algorithm of Quick Sort.
103. Explain the algorithm of Radix Sort.
104. Compare various Sorting Techniques.

• Top 40 Cyber Security Questions and Answers
• Top 10 React JS Interview Theory Questions and Answers
• CISSP – Practice Test Questions – 2024 – Set 20 (53 Questions)
• Part 2: Exploring Deeper into CCNA – Wireless (145 Practice Test Questions)
• Part 1: Mastering CCNA – Wireless (145 Practice Test Questions)
• [1z0-1085-20] Oracle Cloud Infrastructure Foundations 2020 Associate MCQ Questions – Part 3
• [1z0-1085-20] Oracle Cloud Infrastructure Foundations 2020 Associate MCQ Questions – Part 2
• [1z0-1085-20] Oracle Cloud Infrastructure Foundations 2020 Associate MCQ Questions – Part 1
• 1Z0-931 – Oracle Autonomous Database Cloud Specialist Questions – Part 2
• 1Z0-931 – Oracle Autonomous Database Cloud Specialist Questions – Part 1